먼저 쌍곡선의 정의부터 알아봅시다.
쌍곡선의 정의는 "두 정점으로 부터 거리의 차가 일정한 점들의 집합"입니다.
좌표평면에서 예를 들어볼게요. 두 정점을 F와 F'이라고 하고 아무 위치에나 찍겠습니다. 이 두 점으로부터 거리의 차가 일정한 점들을 찍으면 쌍곡선이 됩니다.
다행히 고등학교 과정에서는 정점을 아무 위치에나 찍지는 않구요. x축과 y축에 평행한 직선 위에 찍습니다. 단순한 형태만 다루자는 것이지요.
1. 두 초점이 x축에 있는 경우
x축 위에 두 정점이 찍힌 경우를 생각해 봅시다. 두 정점은 원점 대칭의 위치에 찍겠습니다. F(c,0) 과 F'(-c,0) 입니다. 이 두 정점은 '초점'이라고 부릅니다. 그리고 이 초점으로 부터 거리의 차가 일정한 점들로 만들어진 쌍곡선을 하나 그리겠습니다.

쌍곡선이이 x축과 만나는 두 점을 (a,0)와 (-a,0)로 놓겠습니다. 이 두점을 쌍곡선의 꼭지점이라고 부릅니다.
점 (a,0)에서도, 두 정점 F와 F' 로 부터의 거리의 차이가 일정하겠지요? 그 값을 구해봅시다. 초점F에서 a까지의 거리는 c-a 구요. 초점F'에서 a꺼지의 거리는 c+a입니다. 거리의 차를 구해봅시다. c+a에서 c-a를 뺍니다. 거리의 차이는 2a와 같습니다.
이제 쌍곡선의 방정식을 유도해봅시다. 쌍곡선 위의 임의의 점을 P(x,y)라고 놓겠습니다. 점 P와 초점 사이의 거리를 아래와 같이 나타낼 수 있습니다.
$l_{1}=\sqrt{ (x+c)^{2}+y^{2}}$
$l_{2}=\sqrt{ (x-c)^{2}+y^{2}}$
두 거리의 차는 2a와 같기 때문에 아래 등식이 성립합니다.
$\left | l_{1}-l_{2} \right | = 2a$
절댓값을 벗겨줍니다.
$ l_{1}-l_{2} = \pm 2a$
$l_{1}$과 $l_{2}$를 아래와 같이 변형합니다.
$\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}= \pm 2a$
아래와 같이 이항합니다.
$-\sqrt{(x-c)^{2}+y^{2}}=-\sqrt{(x+c)^{2}+y^{2}} \pm 2a$
양변을 제곱합니다.
$(x-c)^{2}+y^{2}=(x+c)^{2}+y^{2}\mp 4a\sqrt{ (x+c)^{2}+y^{2} }+4a^{2}$
제곱식을 정리하고 소거할 수 있는 항은 합니다.
$-2xc=2xc \mp 4a\sqrt{ (x+c)^{2}+y^{2} }+4a^{2}$
아래와 같이 이항합니다.
$\pm 4a\sqrt{ (x+c)^{2}+y^{2} }=4a^{2}+4xc$
4로 약분합니다.
$\pm a\sqrt{ (x+c)^{2}+y^{2} }= a^{2}+xc$
양변을 제곱합니다.
$a^{2}\left \{ (x+c)^{2}+y^{2} \right \}= a^{4}+2a^{2}xc+x^{2}c^{2}$
좌변을 전개합니다.
$a^{2}x^{2}+2a^{2}xc+a^{2}c^{2}+a^{2}y^{2}= a^{4}+2a^{2}xc+x^{2}c^{2}$
소거할 수 있는 항은 소거합니다.
$a^{2}x^{2}+a^{2}c^{2}+a^{2}y^{2}= a^{4}+x^{2}c^{2}$
x,y와 관련된 항만 좌변으로 모아줍니다.
$a^{2}x^{2}-x^{2}c^{2}+a^{2}y^{2}= a^{4}-a^{2}c^{2}$
공통 인수로 묶어줍니다.
$\left ( a^{2}-c^{2} \right )x^{2}+a^{2}y^{2}= a^{2}\left ( a^{2}-c^{2} \right )$
양변에 -1을 곱해줍니다.
$\left ( c^{2}-a^{2} \right )x^{2}-a^{2}y^{2}= a^{2}\left ( c^{2}-a^{2} \right )$
아래와 같이 치환을 해줍니다.
$b^{2}=c^{2}-a^{2}$
위 식에 적용합시다.
$b^{2}x^{2}-a^{2}y^{2}= a^{2}b^{2}$
양변을 $a^{2}b^{2}$으로 나눠줍니다.
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
유도한 수식이 두가지 쌍곡선의 방정식중 하나입니다. 초점이 x축 위에 있는 쌍곡선의 방정식입니다. 타원의 방정식이랑 비슷하게 생겼죠?
타원의 방정식에서는 b의 기하학적인 의미를 처음부터 알 수 있었어요. y절편이었죠. 쌍곡선에서 b의 의미는 뒷부분에서 설명하도록 하겠습니다.
2. 두 초점이 x축에 있는 쌍곡선의 점근선의 방정식
위 수식을 y에 대해 정리해봅시다. 아래와 같이 이항해줍니다.
$\frac{y^{2}}{b^{2}}=\frac{x^{2}}{a^{2}}-1$
양변에 $b^{2}$을 곱합니다.
$y^{2}=\frac{b^{2}}{a^{2}}\ x^{2}-b^{2}$
양변에 루트를 씌웁니다.
$y=\pm\sqrt{ \frac{b^{2}}{a^{2}}\ x^{2}-b^{2}}$
아래와 같이 루트 안을 묶어줍니다.
$y=\pm\sqrt{ \frac{b^{2}}{a^{2}}\ x^{2}\left ( 1-\frac{a^{2}}{x^{2}} \right )}$
제곱항을 루트 밖으로 꺼내줍니다.
$y=\pm \frac{b}{a} \ x \sqrt{ \left ( 1-\frac{a^{2}}{x^{2}} \right )}$
x가 무한대로 간다면 아래와 같이 수렴합니다. x가 무한대로 갈 때 쌍곡선이 아래 직선으로 가까워져간다는 것입니다. 이 직선을 '점근선'이라고 부릅니다. 점점 가까워져가는 선입니다.
$y=\pm \frac{b}{a} \ x $
그렇다면 b의 의미는 무엇일까요. b는 점근선의 방정식의 x 값이 a 일 때, y 값입니다.
3. 두 정점이 y축에 있는 경우
이번에는 두 정점을 y축에 찍어봅시다. 이 점을 '초점'이라고 불렀었어요. F(0,c)와 F'(0,-c)입니다. 이 두 점으로 부터 거리의 차가 일정한 점들을 찍으면 쌍곡선이 됩니다. y축과 만나는 점을 (0,b) 와 (0,-b) 라고 놓겠습니다.
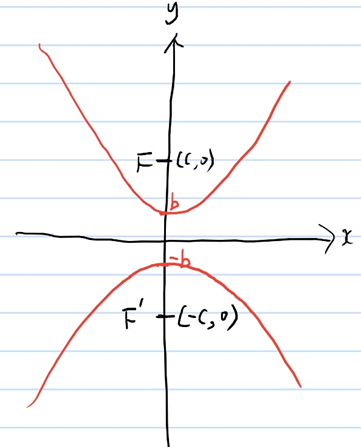
두 초점에서 (0,b)에 그은 직선에 길이의 합을 구해봅시다. F에서 (0,b)까지의 길이는 c-b 이구요. F'에서 (0,b)까지의 거리는 b+c 입니다. b+c에서 c-b를 빼면 2b가 나옵니다. 거리의 차이가 2b와 같습니다.
이제 쌍곡선의 방정식을 유도해봅시다. 쌍곡선 위의 임의의 점을 P(x,y)라고 놓겠습니다. 점 P와 초점 사이의 거리를 아래와 같이 나타낼 수 있습니다.
$l_{1}=\sqrt{ x^{2}+(y-c)^{2}}$
$l_{2}=\sqrt{ x^{2}+(y+c)^{2}}$
두 거리의 차는 2b와 같기 때문에 아래 등식이 성립합니다.
$\left | l_{1}-l_{2} \right | = 2b$
절댓값을 벗겨줍니다.
$ l_{1}-l_{2} = \pm 2b$
$l_{1}$과 $l_{2}$를 아래와 같이 변형합니다.
$\sqrt{x^{2}+(y-c)^{2}}-\sqrt{x^{2}+(y+c)^{2}}= \pm 2b$
가장 왼쪽에 있는 항을 이항하고 아래와 같이 변형합니다.
$-\sqrt{x^{2}+(y+c)^{2}}=-\sqrt{x^{2}+(y-c)^{2}} \pm 2b$
양변을 제곱합니다.
$x^{2}+(y+c)^{2}=x^{2}+(y-c)^{2} \mp 4b\sqrt{x^{2}+(y-c)^{2}}+4b^{2}$
전개하고 소거가능한 항은 소거합니다.
$2cy=-2cy \mp 4b\sqrt{x^{2}+(y-c)^{2}}+4b^{2}$
4로 약분합니다.
$\pm b\sqrt{x^{2}+(y-c)^{2}} =b^{2}-cy$
양변을 제곱합니다.
$b^{2} \left \{ x^{2}+(y-c)^{2} \right \}=b^{4}-2b^{2}yc+c^{2}y^{2}$
좌변을 전개합니다.
$b^{2}x^{2}+b^{2}y^{2}-2b^{2}yc+b^{2}c^{2}=b^{4}-2b^{2}yc+c^{2}y^{2}$
아래와 같이 소거합니다.
$b^{2}x^{2}+b^{2}y^{2}+b^{2}c^{2}=b^{4}+c^{2}y^{2}$
x,y와 관련된 항만 좌변으로 모아줍니다.
$b^{2}x^{2}+b^{2}y^{2}-c^{2}y^{2}=b^{4}-b^{2}c^{2}$
공통 인수로 묶어줍니다.
$b^{2}x^{2}+\left ( b^{2}-c^{2} \right )y^{2}=\left ( b^{2}-c^{2} \right )b^{2}$
아래와 같이 치환합니다.
$a^{2}=c^{2}-b^{2}$
위 식에 대입합니다.
$b^{2}x^{2}-a^{2}y^{2}=-b^{2}a^{2}$
양변을 $a^{2}b^{2}$으로 나눠줍니다.
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=-1$
유도한 수식이 초점이 y축 위에 있는 쌍곡선의 방정식입니다.
4. 두 초점이 y축에 있는 쌍곡선의 점근선의 방정식
위 수식을 y에 대해 정리해봅시다.
$\frac{y^{2}}{b^{2}}=\frac{x^{2}}{a^{2}}+1$
양변에 $b^{2}$을 곱합니다.
$y^{2}=\frac{b^{2}}{a^{2}} \ x^{2}+b^{2}$
양 변에 루트를 씌웁니다.
$y=\pm \sqrt{\frac{b^{2}}{a^{2}} \ x^{2}+b^{2}}$
아래와 같이 루트 안을 묶어줍니다.
$y=\pm \sqrt{\frac{b^{2}}{a^{2}} \ x^{2}\left ( 1+\frac{b^{2}}{x^{2}} \right )}$
루트를 벗겨줍니다.
$y=\pm \frac{b}{a} \ x \ \sqrt{ \left ( 1+\frac{b^{2}}{x^{2}} \right )}$
x가 무한대로 간다면 아래와 같이 수렴합니다.
$y=\pm \frac{b}{a} \ x $
x가 무한대로 갈 때 쌍곡선이 아래 직선으로 가까워져간다는 것입니다. 이 직선을 '점근선'이라고 부릅니다. 점점 가까워져가는 선입니다.
5. 정리
두 가지 쌍곡선의 방정식을 유도했습니다.
<초점이 x축에 있는 경우>
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
<초점이 y축에 있는 경우>
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=-1$
두 쌍곡선은 같은 점근선의 방정식을 갖습니다. 초점의 좌표 값의 크기도 같구요.
'고등수학 5분증명(2009개정) > 기하와 벡터' 카테고리의 다른 글
| [5분 고등수학] 포물선의 접선의 방정식(포물선 밖의 한점) (0) | 2022.04.14 |
|---|---|
| [5분 고등수학] 포물선의 접선의 방정식(포물선 위의 한점) (0) | 2022.04.13 |
| [5분 고등수학] 음함수의 미분 (0) | 2022.04.12 |
| [5분 고등수학 ] 쌍곡선의 방정식의 평행이동과 일반형 (0) | 2022.04.11 |
| [5분 고등수학] 타원의 방정식의 평행이동과 일반형 (0) | 2022.04.07 |
| [5분 고등수학] 타원의 방정식 유도 (2) x축 위에 두 초점이 있는 경우 (0) | 2022.04.06 |
| [5분 고등수학] 타원의 방정식 유도 (1) x축 위에 두 초점이 있는 경우 (0) | 2022.04.05 |
| [5분 고등수학] 포물선 방정식의 평행이동과 일반형 (0) | 2022.04.04 |

댓글