지난 강의에 이어서 두 정점이 y축 위에 있는 경우 타원의 방정식을 유도해봅시다.
2) 두 정점이 y축 위에 있는 경우
두 정점을 y축 위에, 원점 대칭으로 찍겠습니다. 정점 F의 좌표는 (0,c)이고, F'의 좌표는 (0,-c)입니다.
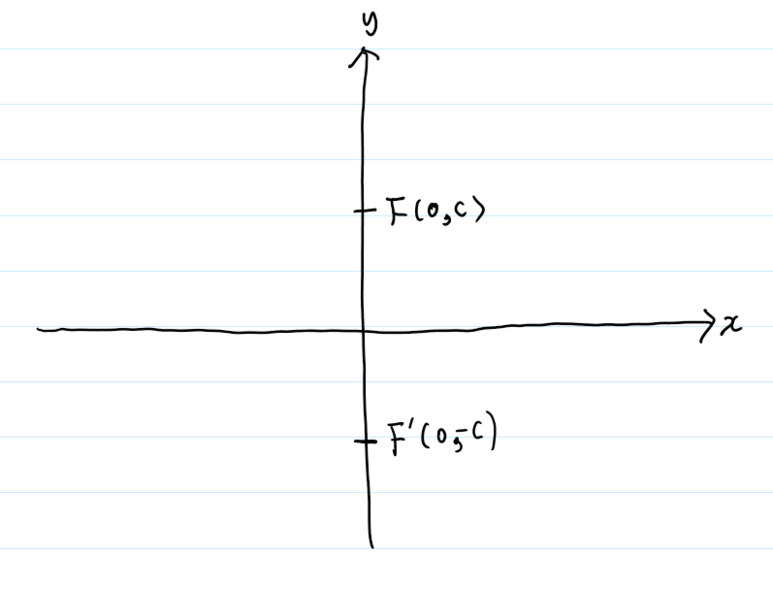
이 정점들로 부터 거리의 합이 일정한 점들로 이루어진 타원을 그리겠습니다. 이 타원이 x축과 만나는 점을 (a,0)과 (-a,0)이라고 합시다. y축과 만나는 점을 (0,b)와 (0,-b)라고 놓겠습니다. 이 네개의 점을 타원의 '꼭지점'이라고 합니다.

타원의 정의에 의해 점 (0,b)에서도 두 정점으로 부터의 거리의 합이 일정합니다. 그 값을 b로 표현해봅시다.
먼저 정점 F로 부터 (0,b)에 이르는 거리는 (b-c)입니다. 정점 F'으로 부터 (0,-b)에 이르는 거리는 (b+c)입니다. 둘을 더하면 2b가 됩니다.
이번에는 a,b,c의 관계를 알아봅시다. 두 정점에서 (a,0)에 선을 그어봅시다.

위에 그은 빨간 두 선의 길이의 합도 2b가 됩니다. 수식을 세우면 아래와 같습니다. 피타고라스 정리를 사용합니다.
$2\sqrt{{a}^2+{c}^2}=2b$
양변을 제곱하여 정리하면 아래와 같습니다.
${a}^2+{c}^2={b}^2$
위 식을 통해 b가 항상 a보다 크다는 것을 알 수 있습니다. 이제 용어 몇가지를 정의해봅시다.
처음에 찍은 두 정점 F와 F'을 '초점'이라고 부릅니다. 타원의 두 축을 그을 수 있는데요. 한 축의 길이는 2a이고, 다른 한 축의 길이는 2b입니다. b가 a보다 항상 크기 때문에 길이가 2b인 축을 를 장축, 2a인 축을 단축이라고 부릅니다.
이제 타원의 방정식을 유도해봅시다. 타원 위 임의의 점을 P(x,y)라고 놓읍시다. 타원의 정의를 이용하면 아래와 같은 등식을 만들 수 있습니다. 두 초점에서 P까지 이르는 거리의 합이 2b라는 등식입니다.
$\sqrt{{x}^2+{\left(y-c\right)}^2}+\sqrt{x^2+{\left(y+c\right)}^2}=2b$
아래와 같이 이항합시다.
$\sqrt{{x}^2+{\left(y-c\right)}^2}=2b-\sqrt{x^2+{\left(y+c\right)}^2}$
양변을 제곱합시다.
${x}^2+{\left(y-c\right)}^2=4{b}^2-4b\sqrt{{x}^2+{\left(y+c\right)}^2}+{x}^2+{\left(y+c\right)}^2$
전개합시다.
${x}^2+{y}^2-2cy+{c}^2=4{b}^2-4b\sqrt{x^2+{\left(y+c\right)}^2}+{x}^2+{y}^2+2cy+{c}^2$
정리합시다.
$-4cy-4{b}^2=-4b\sqrt{{x}^2+{\left(y+c\right)}^2}$
양변을 -4로 나눕시다.
$cy+{b}^2=b\sqrt{{x}^2+{\left(y+c\right)}^2}$
다시 양변을 제곱합시다.
${c}^2{y}^2+2{b}^2cy+{b}^4={b}^2\left\{{{x}^2+{\left(y+c\right)}^2}\right\}$
전개합시다.
${c}^2{y}^2+2{b}^2cy+{b}^4={b}^2{x}^2+{b}^2{y}^2+2{b}^2cy+{b}^2{c}^2$
같은 항을 소거합시다.
${c}^2{y}^2+{b}^4={b}^2{x}^2+{b}^2{y}^2+{b}^2{c}^2$
x,y와 관련된 항을 좌변에 나머지 항을 우변에 정리합시다.
${c}^2{y}^2-b^2{x}^2-{b}^2{y}^2={b}^2{c}^2-{b}^4$
아래와 같이 묶어줍니다.
$-{{b}^2}{x}^2+\left({c}^2-{b}^2\right){y}^2=\left({{c}^2-{b}^2}\right){b}^2$
우리는 위에서 아래 등식일 성립한다는 것을 배웠습니다.
${c}^2-{b}^2=-{a}^2$
대입합시다.
$-{b}^2{x}^2-a^2{y}^2=-{a}^2{b}^2$
양변을 -a²b² 으로 나눠줍니다.
$\frac{{x}^2}{{a}^2}+\frac{{y}^2}{{b}^2}=1$
y축위에 두 초점을 갖고, x축 대칭인 타원의 방정식이 유도되었습니다.
지난 강의에서 유도한 타원의 방정식과 모양은 동일합니다. y축 위에 초점이 있는지 x축에 초점이 있는지 어떻게 구분할까요?? a와 b의 크기를 비교하면 됩니다. a가 b보다 크다면 x축 위에 초점이 있는 것이고, b가 a보다 크다면 y축 위에 초점이 있는 것입니다.
'고등수학 5분증명(2009개정) > 기하와 벡터' 카테고리의 다른 글
| [5분 고등수학] 음함수의 미분 (0) | 2022.04.12 |
|---|---|
| [5분 고등수학 ] 쌍곡선의 방정식의 평행이동과 일반형 (0) | 2022.04.11 |
| [5분 고등수학] 쌍곡선의 방정식의 유도 (0) | 2022.04.08 |
| [5분 고등수학] 타원의 방정식의 평행이동과 일반형 (0) | 2022.04.07 |
| [5분 고등수학] 타원의 방정식 유도 (1) x축 위에 두 초점이 있는 경우 (0) | 2022.04.05 |
| [5분 고등수학] 포물선 방정식의 평행이동과 일반형 (0) | 2022.04.04 |
| [5분 고등수학] 포물선의 방정식 유도 (0) | 2022.04.01 |
| [5분 고등수학] 이차곡선 한눈에보기 (0) | 2022.03.31 |


댓글