미분은 함수의 접선의 기울기를 구하는 것입니다. 우리는 미분을 이해하고 있다고 생각하지만 사실은 아닐 수도 있습니다. 오늘은 미분이 가지고 있는 모순에 대해 이야기해보려고 합니다.
먼저 미분의 원리를 알아보기 위해 간단한 함수를 가지고 접선의 기울기를 구해봅시다. 아래와 같은 2차함수가 있다고 합시다. $y=x^2$ 입니다.

점 A에서의 접선의 기울기를 구해볼 것입니다. A보다 값이 큰 점 B를 하나 더 설정합니다.

이제 A와 B를 연결한 직선을 만들어줍니다.
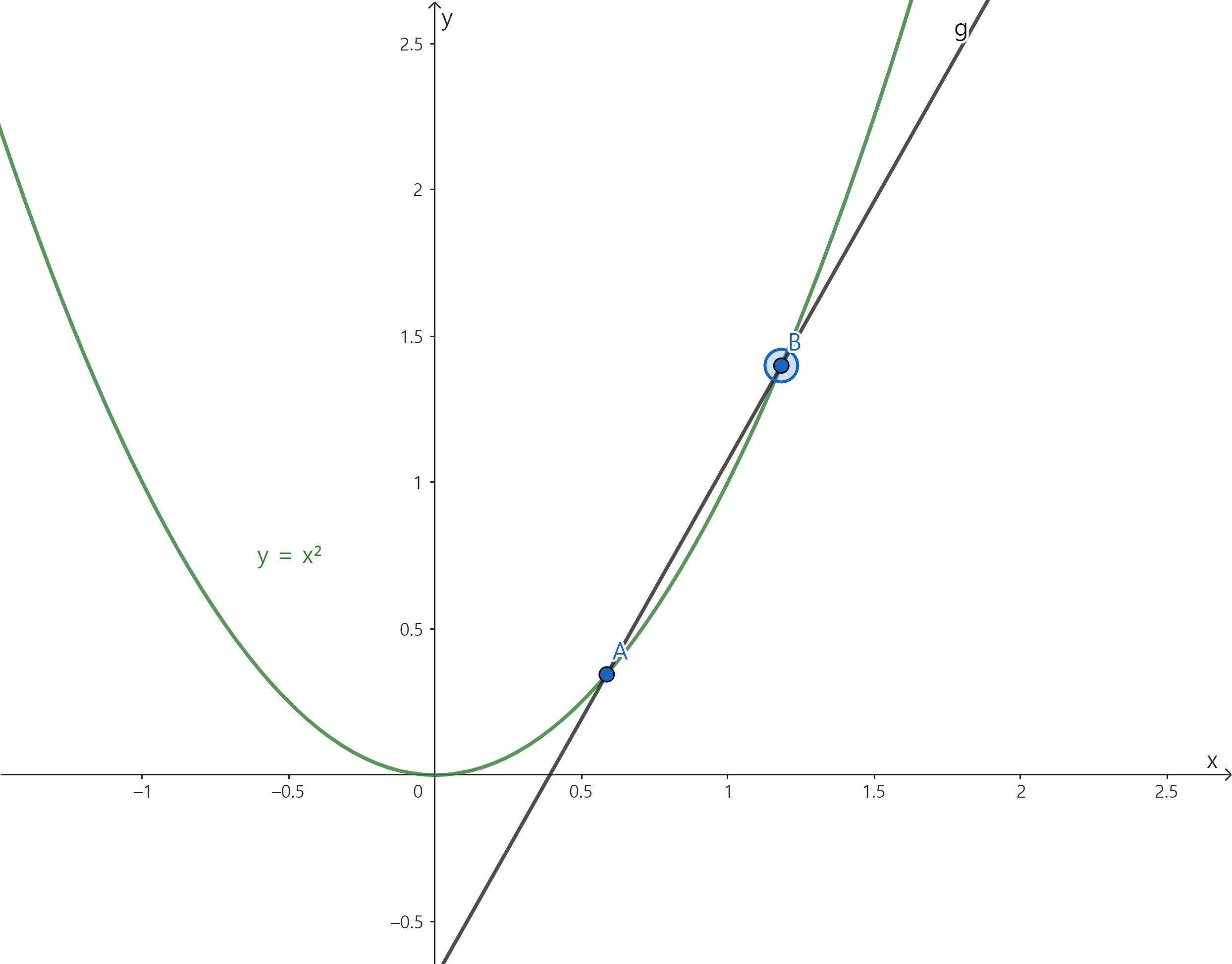
이 직선의 기울기를 수식으로 표현한 뒤, 점 B를 점점 A에 가깝게 만들어주다 보면 기울기가 A의 접선의 기울기에 가까워져 갑니다.
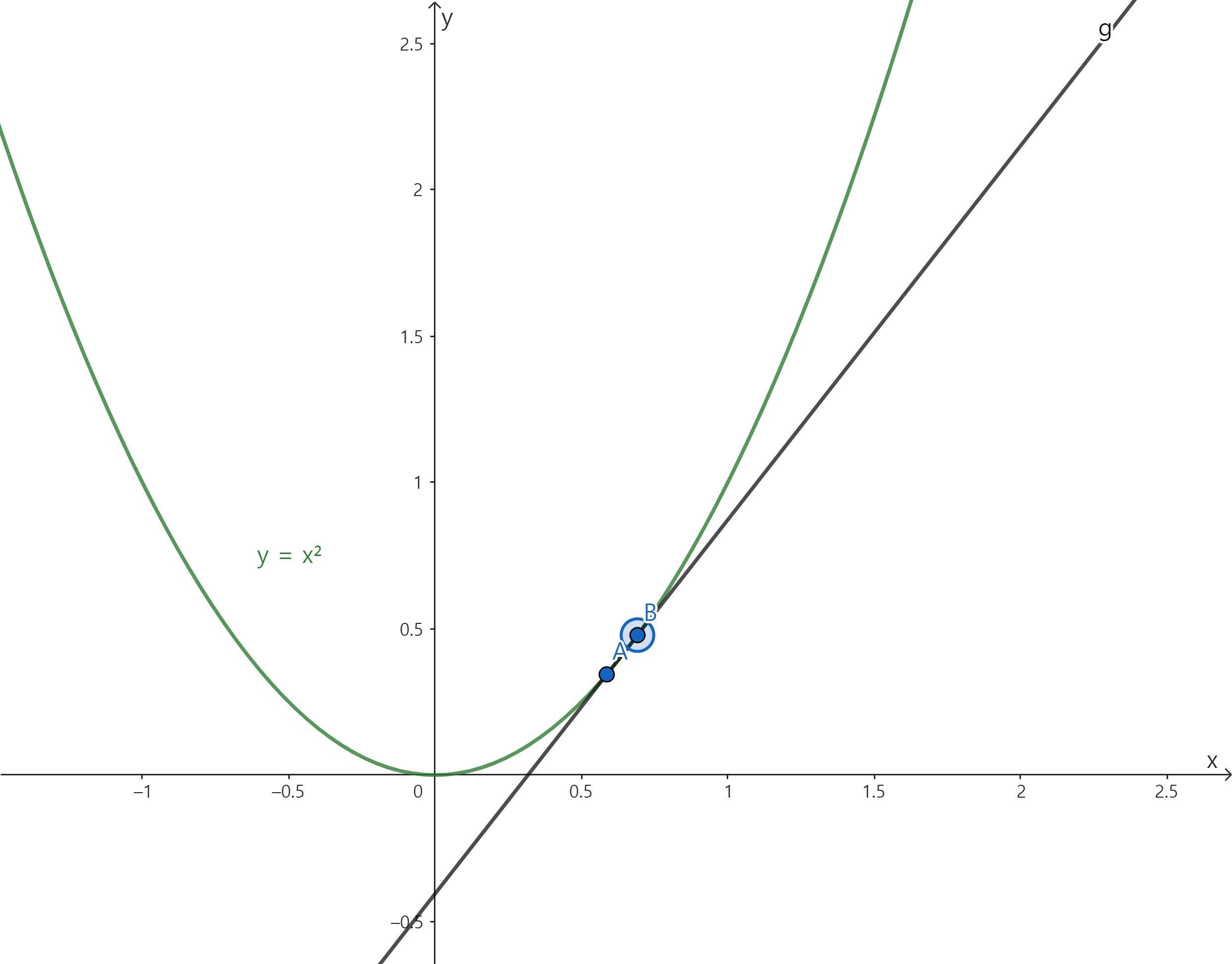
위 상황을 수식으로 표현해봅시다. 점 A의 좌표를 $(a,a^2)$ 이라고 놓겠습니다. 점 B의 좌표는 $(a+h, (a+h)^2)$ 이라고 놓겠습니다. 이때 직선 AB의 기울기는 아래와 같이 표현됩니다.
직선 AB의 기울기 = $\frac{(a+h)^2-a^2 }{a+h-a}$
분자를 전개해줍시다.
직선 AB의 기울기 = $\frac{a^2+2ah+h^2-a^2 }{a+h-a}$
아래와 같이 분자와 분모를 계산합니다.
직선 AB의 기울기 = $\frac{2ah+h^2 }{h}$
위 식에서 h가 0이 아니라고 가정하면 아래와 같이 약분할 수 있습니다.
직선 AB의 기울기 = $2a+h $
점 A에서의 접선의 기울기는 h가 0일 때의 기울기인 2a 입니다. 그런데 우리는 h가 0이 아니라는 가정을 하고 약분을 했습니다. 따라서 h는 0일 수 없습니다. 약분하기 전으로 돌아가봅시다.
직선 AB의 기울기 = $\frac{2ah+h^2 }{h}$
h는 분모에 있으므로 0이 될 수 없습니다. 점 A에서의 접선의 기울기가 2a라고 하려면 h가 0이 아니었다가, 다시 0이 되는 이상한 일이 벌어져야 합니다. 우리가 알고 있던 미분이 왜이런 걸까요?
'etc > 어려운 수학이야기' 카테고리의 다른 글
| 고윳값과 고유벡터 쉽게 이해하기 (0) | 2023.08.09 |
|---|---|
| 행렬형태의 연립방정식을 이해하는 세가지 관점 (0) | 2023.08.08 |
| 다각형의 넓이를 구하는 방법 (모든 다각형 가능, +코딩) (0) | 2023.06.20 |
| [좌표 변환] 글로벌 좌표를 로컬좌표로, 또는 그 반대 (0) | 2023.05.29 |
| [벡터의 회전과 행렬] (1) 2차원 평면 (0) | 2023.05.24 |
| 미분과 극한 제대로 이해하기 (3) 극한을 엄밀하게 정의한 입실론-델타 (0) | 2023.01.30 |
| 미분과 극한 제대로 이해하기 (2) 극한의 등장 (0) | 2023.01.30 |



댓글