반응형
무리수는 순환하지 않는 무한소수입니다. 대표적으로는 $\pi$ , e , $\sqrt{2}$ 가 있습니다. 파이는 3.141592..... 와 같이 소숫점 이후 자릿수가 끝없이 계속됩니다.
이런 이유 때문에 마치 무리수가 어딘가로 다가가는 중인 수라고 생각하시는 경우가 있습니다. 움직이는 상태인 수라고 생각하는 겁니다. 파이는 3.14 로 시작하여 3.14159265358979... 로 어딘가를 향해 다가가는 중이라고 말이죠.
오늘 이 오해를 풀어보겠습니다. 무리수는 어딘가로 다가가는 수가 아니라 멈춰있는 수 입니다. 크기가 얼마로 딱 정해진 수인 것입니다. $\sqrt{2}$를 생각해봅시다. $\sqrt{2}$는 아래와 같이 밑변과 높이가 1인 삼각형의 대각선 길이입니다.
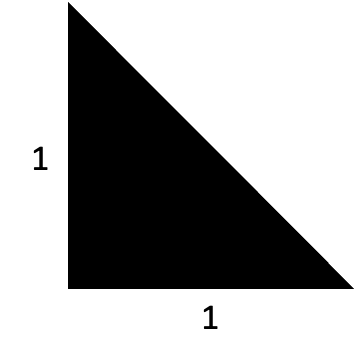
파이도 마찬가지입니다. 파이는 지름의 길이가 1인 원의 둘레의 길이입니다. 고정되어 있는, 멈춰있는 값입니다.

무리수는 움직이지 않습니다.
반응형
'etc > 쉬운 수학이야기' 카테고리의 다른 글
| 미분해서 자기 자신이 나오는 함수는 e^x 가 유일할까? 3편 (0) | 2022.10.20 |
|---|---|
| 미분해서 자기 자신이 나오는 함수는 e^x 가 유일할까? 2편 (0) | 2022.10.15 |
| 대수학은 왜 알제브라(algebra) 일까 (0) | 2022.10.13 |
| 수학선생님들은 어떤 시험을 본걸까 (임용고시 과목) (1) | 2022.10.13 |
| 미분해서 자기 자신이 나오는 함수는 e^x 가 유일할까? 1편 (0) | 2022.10.10 |
| 1/x 를 적분하면 왜 ln|x| 일까 (절댓값이 왜 생길까) (1) | 2022.10.10 |
| 중고등학교에서 배운 기하학 vs 비유클리드기하학 (0) | 2022.10.02 |
| 라마누잔이 천재임을 증명하는 일화? (0) | 2022.09.29 |
댓글