반응형
1. 직선과 평면이 이루는 각
α라는 평면이 있고, 이 평면위에 있지 않은 직선 l이 있습니다.

직선 l과 만나는 점을 A라고 하고, l위의 한 점을 B라고 할게요. 이 점 B에서 평면 α에 내린 수선의 발을 B'라고 하겠습니다.
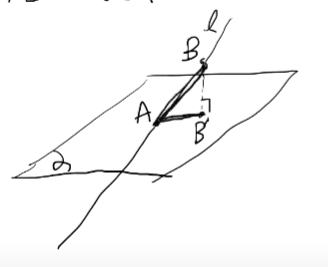
이때, 직선 l과 선문 AB'가 이루는 각 $\theta$가 직선l과 평면α 사의 각입니다.

2. 이면각
이면각은 두 면 사이의 각입니다. 한자로 둘(이)에요. 이면각이 어떻게 정의되는지를 알아야합니다. 두 면이 평행하지 않다면 한 선에서 만납니다.

이 선 위에 있는 한점으로 부터 이 선에 수직하고 각 면 위에 있는 선을 그을 수 있습니다. 이 두 선 사이의 각도가 이면각입니다.

반응형
'고등수학 5분증명(2009개정) > 기하와 벡터' 카테고리의 다른 글
| [5분 고등수학] 두 직선이 이루는 각의 크기 (0) | 2022.05.12 |
|---|---|
| [5분 고등수학] 공간에서의 직선의 방정식 (0) | 2022.05.11 |
| [5분 고등수학] 구의 방정식 (0) | 2022.05.10 |
| [5분 고등수학] 정사영 (0) | 2022.05.09 |
| [5분 고등수학] 삼수선의 정리 (0) | 2022.05.04 |
| [5분 고등수학] 곡선의 길이 (0) | 2022.05.03 |
| [5분 고등수학] 평면 위 운동에서 점이 움직인 거리 (0) | 2022.05.02 |
| [5분 고등수학] 평면운동에서의 속도와 가속도 (0) | 2022.04.29 |


댓글