반응형
삼각형 ABC의 무게중심을 G라고 하겠습니다.

네개의 위치벡터를 정의할 수 있습니다. 점 A,B,C,G 의 위치벡터입니다. 이 위치벡터들을 $\vec{a}$, $\vec{b}$, $\vec{c}$, $\vec{g}$ 라고 하겠습니다.
무게중심의 위치를 찾아봅시다. 변 BC의 중점을 M이라고 하겠습니다. 이때, 변 AM를 2:1로 내분하는 점이 무게중심입니다.
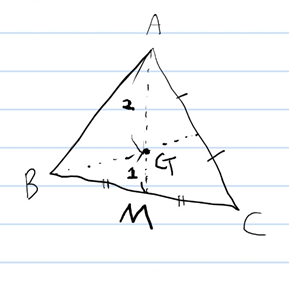
변 BC의 중점의 위치벡터는 아래와 같습니다.
$\overrightarrow{OM}=\frac{\vec{b}+\vec{c}}{2}$
AM을 2:1로 내분하는 점 G의 위치벡터 아래와 같습니다.
$\overrightarrow{OG}=\frac{ 2 \overrightarrow{OM} + \overrightarrow{OA} }{3}$
아래와 같이 변형합니다.
$\overrightarrow{OG}=\frac{2}{3}\frac{\vec{b}+\vec{c}}{2}+\frac{\vec{a}}{3}$
정리하면 아래와 같습니다.
$\overrightarrow{OG}=\frac{ \vec{a}+\vec{b}+\vec{c} }{3}$
반응형
'고등수학 5분증명(2009개정) > 기하와 벡터' 카테고리의 다른 글
| [5분 고등수학] 원의 벡터방정식 (0) | 2022.04.28 |
|---|---|
| [5분 고등수학] 직선의 벡터 방정식 (0) | 2022.04.27 |
| [5분 고등수학] 벡터의 내적과 성분 (0) | 2022.04.26 |
| [5분 고등수학] $\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$ 인 점 P의 자취 (0) | 2022.04.25 |
| [5분 고등수학] 선분의 내분점과 외분점의 위치벡터 (0) | 2022.04.21 |
| [5분 고등수학] 두 벡터의 평행조건, 세 점이 한 직선 위에 있을 조건 (0) | 2022.04.20 |
| [5분 고등수학] 쌍곡선의 접선의 방정식(쌍곡선 밖의 한점) (0) | 2022.04.19 |
| [5분 고등수학] 쌍곡선의 접선의 방정식(쌍곡선 위의 한점) (0) | 2022.04.18 |
댓글