여섯사람이 우주선을 타고 우주를 항해하고 있었습니다. 그러던 어느 날 갑자기 우주선에 불이 난 겁니다. 우주선에서 탈출해야하는 상황이 되었습니다. 우주선에는 만일의 사태를 대비해서 우주선을 탈출할 수 있는 탈출선이 하나 있었어요. 그런데 설계자가 실수로 세사람만 타고 나갈 수 있도록 설계를 한 겁니다. 여섯명중 세사람은 탈출할 수 있고, 세 사람은 우주선에 남아서 죽어야 하는 슬픈 상황입니다.
여섯사람은 모여서 회의를 했습니다. 어떻게 하면 공정하게 탈출할 사람을 정할 수 있을까 회의한 결과 제비뽑기를 하기로 했습니다. 제비뽑기 방식은 이렇습니다.
종이에 사람의 이름을 적습니다. 사람 이름은 A,B,C,D,E,F 라고 하겠습니다. 종이에 세 사람의 이름을 적는데, 모든 경우의 수 만큼의 종이를 준비하고 이름을 적는겁니다.
종이1 - A,B,C
종이2 - A,B,D
...
이렇게요.
그리고 모든 종이를 접어서 상자에 넣고, 섞습니다. 한 사람이 종이를 뽑고, 처음 나온 종이에 적힌 사람 세명이 탈출선을 타기로 했습니다.
이때, 필요한 쪽지의 개수를 구해봅시다.
탈출선의 첫번째 자리를 1번, 두번째 자리를 2번, 세번째 자리를 3번이라고 해봅시다.
첫번째 자리에 A가 타면, 두번째 자리에 탈 수 있는 사람은 B,C,D,E,F 입니다.
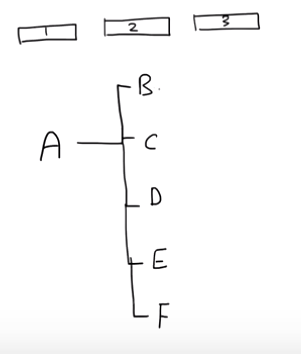
두번째 자리에 B가 타면, 세번째 자리에 탈 수 있는 사람은 C,D,E,F입니다.
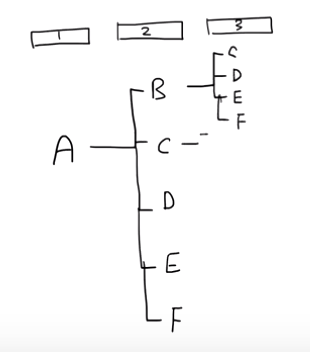
두번째 자리에 다른 사람이 타도, 세번째 자리에 탈 수 있는 사람의 경우의 수는 네가지입니다. 두번째 자리에 올 수 있는 다섯가지 경우가 각각 네가지 경우로 나눠지니까 총 20가지 경우가 됩니다.
4(두번째 자리에 사람이 타는 경우의 수) X 5(세번째 자리에 사람이 타는 경우의 수) = 20
첫번째 자리에 A가 왔을 때 만들어지는 쪽지 개수가 20가지입니다. 그런데 첫번째 자리에는 A뿐만 아니라 B,C,D,E도 올 수 있습니다. 첫번째 자리에 사람이 타는 경우의 수는 6가지 입니다. 따라서 20에 6을 더 곱해주어야 전체 쪽지 수가 구해집니다.
6(첫번째 자리에 타는 사람의 경우의 수) X5(두번째 자리) X 4(세번째 자리) = 120
이렇게 쪽지를 120개 만들어야 합니다. 우리가 지금 구한 쪽지의 개수가 '순열'입니다. 어떤 순열을 계산한 것인지 자세히 말씀드릴게요.
'6명의 사람 중에서 세명을 뽑아서 일렬로 배열' 하는 순열을 계산한 것입니다. 기호로는 아래와 같이 표현합니다.
$_{6}P_{3}$
p는 '순열'이라는 뜻의 permutation 의 첫글자입니다. p 의 왼쪽에는 전체 사람 수, p의 오른쪽에는 뽑아서 일렬로 나열할 사람의 수를 써줍니다.
몇가지 예를 들어봅시다.
$_{5}P_{2}$
위 수식은 우주선에 탑승한 사람이 5명이고, 자리가 2자리인 상황에서 계산한 종이의 수 입니다. 아래와 같이 계싼됩니다. 첫번째 자리에 사람이 타는 경우의 수는 5이고, 첫번째 자리에 누군가 탔을 때 두번째 자리에 사람이 타는 경우의 수는 4입니다. 따라서 아래와 같이 계산됩니다.
5x4=20
아래 예시를 봅시다.
$_{10}P_{4}$
위 수식은 우주선에 탑승한 사람이 10명이고, 자리가 4자리인 상황에서 계산한 종이의 수 입니다. 첫번째 자리에 10명이 타고, 두번째 자리에는 9명, 세번째는 8명, 다섯번째는 7명입니다. 따라서 아래와 같이 계산됩니다.
10x9x8x7
이번에는 일반화라는 것을 해봅시다. 아래와 같이 숫자 대신 문자를 넣어 계산하는 것입니다.
$_{n}P_{r}$
먼저 기호를 설명하면, n명 중에서 r명을 뽑아서 일렬로 나열하는 경우의 수입니다. 사람이 아니라 물건이라면, n개 중에서 r개를 뽑아서 일렬로 나열하는 수 입니다.
일반화를 위해서 위에서 계산한 예시들을 다시 뜯어봅시다.
$_{5}P_{2}$
위 수식은 아래와 같이 계산되는 것을 알 수 있습니다.
$_{5}P_{2}=5 \times 4 = \frac{5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}$
다른 예시를 봅시다.
$_{10}P_{4}$
위 수식은 아래와 같이 계산되는 것을 알 수 있습니다.
$_{10}P_{4}=10 \times 9 \times 8 \times 7= \frac{10 \times 9 \times\cdots \times 2 \times 1}{6 \times 5 \times \cdots \times 2 \times 1}$
1부터 n까지 곱한 수를 n!이라는 기호로 놓아봅시다. 위 예시들을 이 기호를 이용하여 표현하면 아래와 같습니다.
$_{5}P_{2}=5 \times 4 = \frac{5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}=\frac{5!}{3!}$
$_{10}P_{4}=10 \times 9 \times 8 \times 7= \frac{10 \times 9 \times\cdots \times 2 \times 1}{6 \times 5 \times \cdots \times 2 \times 1}=\frac{10!}{6!}$
이 규칙을 $_{n}P_{r}$ 에 적용하면 아래와 같습니다.
$_{n}P_{r}=\frac{n!}{(n-r)!}$
위 공식이 n개 중에서 r개를 뽑아 나열했다는 의미인 '순열'입니다.
'고등수학 5분증명(2009개정) > 확률과 통계' 카테고리의 다른 글
| [5분 고등수학] 조합 관련 공식의 직관적 이해 (0) | 2022.02.14 |
|---|---|
| [5분 고등수학] 조합 (0) | 2022.02.11 |
| [5분 고등수학] 같은 것이 있는 순열 (0) | 2022.02.08 |
| [5분 고등수학] 다각형 순열 (0) | 2022.02.07 |
| [5분 고등수학] 원순열 쉽게 이해하기 (관점2) (0) | 2022.01.11 |
| [5분 고등수학] 원순열 쉽게 이해하기 (관점1) (0) | 2022.01.10 |
| [5분 고등수학] 이웃한 순열 쉽게 이해하기 (0) | 2022.01.05 |
| [5분 고등수학] 합의법칙 vs 곱의법칙 쉽게 이해하기 (0) | 2022.01.03 |



댓글