오늘 배워볼 내용은 아래 두가지 정리입니다.
1) 최대 최소의 정리
2) 중간값(사잇값)정리
두 내용은 고등학교 수학 수준에서는 증명이 불가능합니다. 의미만 이해할 수 있습니다.
1) 최대 최소의 정리
최대최소의 정리는 아래와 같습니다.
함수 f(x)가 닫힌구간 [a,b]에서 연속이면 f(x)는 반드시 최댓값과 최솟값을 갖는다.
어떤 의미인지 그래프를 통해 이해해봅시다. 함수 f(x)가 닫힌구간 [a,b]에서 연속이라면 아래와 같은 형태의 그래프입니다.

구간 내에 발산하는 곳이 없기 때문에 최댓값과 최솟값은 항상 존재합니다.

그림으로 보면 너무 당연한데, 당연한 내용일 수록 증명이 어렵습니다.
함수가 구간 [a,b]에서 연속이 아니면 최대최소 정리는 성립하지 않습니다. 아래 함수는 구간 [a,b]에서 최댓값이 없습니다.

2) 중간값(사잇값)정리
중간값(사잇값)정리는 아래와 같습니다.
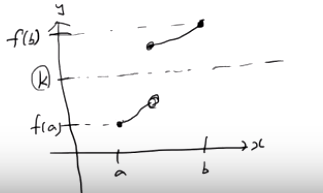
함수 f(x)가 닫힌구간 [a,b]에서 연속이고 $f(a) \neq f(b)$ 라면, f(a)와 f(b) 사이의 임의의 실수 k에 대하여 $f(c)=k$ 인 c가 열린구간 (a,b)에 적어도 하나 존재한다.
어떤 의미인지 그래프를 통해 이해해봅시다. 함수 f(x)가 닫힌구간 [a,b]에서 연속이라면 아래와 같은 형태의 그래프입니다.

f(a)와 f(b) 사이에 어떤 실수 k가 있다고 합시다.

이때, 함수값이 k인 c가 (a,b)인 구간에 항상 존재한다는 의미입니다.

함수가 구간 [a,b]에서 연속이 아니면 최대최소 정리는 성립하지 않습니다. 아래 함수는 함수값이 k인 c가 (a,b)인 구간에 존재하지 않습니다.
'고등수학 5분증명(2009개정) > 미적분1' 카테고리의 다른 글
| [5분 고등수학] 롤의 정리 (0) | 2021.11.10 |
|---|---|
| [5분 고등수학] 함수 y=f(x)^n 의 미분 유도하기 (0) | 2021.11.09 |
| [5분 고등수학] 도함수의 정의 (0) | 2021.11.08 |
| [5분 고등수학] 미분 가능일 조건 (0) | 2021.11.05 |
| [5분 고등수학] 함수가 연속일 조건 (0) | 2021.11.03 |
| [5분 고등수학] 극한 미정계수 결정 시 사용하는 성질 (1) | 2021.11.02 |
| [5분 고등수학] 함수의 극한값이 존재할 조건 (0) | 2021.11.01 |
| [5분 고등수학] 순환소수 공식 유도 (0) | 2021.10.29 |


댓글