외분점은 '밖에서 나누는 점'이라는 뜻입니다. 외분점은 두 점을 연결하여 만든 선분을 일정한 비율로 나누는 점입니다. 선분 밖에 있는 점으로 말이죠.
먼저 좌표평면 위에 점 두개를 찍어봅시다. 아래 그림과 같이 점 A와 점 B를 찍겠습니다.

선분 를 으로 외분하는 점은 m과 n의 대소관계에 따라 아래와 같이 둘로 나뉩니다. 선분 를 으로 나누는 외분점은 반대편에 생깁니다.

1) 선분 를 으로 외분하는 점 ()
인 경우 선분 를 외분하는 점은 아래 그림의 점 입니다. 아래와 같이 두개의 삼각형을 그릴 수 있습니다.

삼각형의 닮음을 이용하여 비례식을 세우면 아래와 같습니다.
비례식을 풀어봅시다.
전개합시다.
x'으로 정리해야하기 때문에 아래와 같이 이항합니다.
아래와 같이 묶어줍니다.
양변을 (m-n)으로 나눠줍니다.
이번에는 삼각형의 닮음을 이용하여 y축에서 비례식을 세워봅시다.
비례식을 풀어봅시다.
전개합시다.
y'으로 정리해야하기 때문에 아래와 같이 이항합니다.
아래와 같이 묶어줍니다.
양변을 (m-n)으로 나눠줍니다.
인 경우 선분 를 외분하는 점 은 아래와 같습니다.
2) 선분 를 으로 외분하는 점 ()
인 경우 선분 를 외분하는 점은 아래 그림의 점 입니다. 아래와 같이 두개의 삼각형을 그릴 수 있습니다.
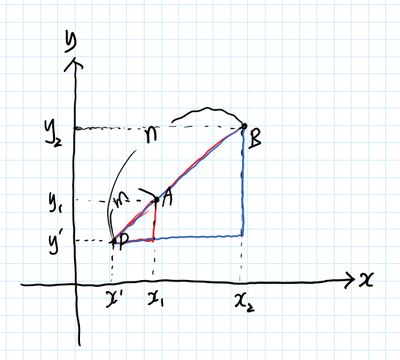
삼각형의 닮음을 이용하여 비례식을 세우면 아래와 같습니다.
비례식을 풀어봅시다.
전개합시다.
x'으로 정리해야하기 때문에 아래와 같이 이항합니다.
아래와 같이 묶어줍니다.
양변을 (m-n)으로 나눠줍니다.
이번에는 삼각형의 닮음을 이용하여 y축에서 비례식을 세워봅시다.
비례식을 풀어봅시다.
전개합시다.
y'으로 정리해야하기 때문에 아래와 같이 이항합니다.
아래와 같이 묶어줍니다.
양변을 (m-n)으로 나눠줍니다.
인 경우 선분 를 외분하는 점 은 아래와 같습니다.
위 두 경우의 외분점이 같습니다. m과 n의 대소관계와 상관없이 선분 를 외분하는 점 은 아래와 같습니다.
'고등수학 5분증명(2009개정) > 수학1' 카테고리의 다른 글
| [5분 고등수학] 점과 직선 사이의 거리 (0) | 2021.07.07 |
|---|---|
| [5분 고등수학] 두 직선의 교점을 지나는 직선 (0) | 2021.07.06 |
| [5분 고등수학] 정점을 지나는 직선 (0) | 2021.07.03 |
| [5분 고등수학] 두 직선이 수직일 때의 기울기 (0) | 2021.06.26 |
| [5분 고등수학] 선분의 내분점 (0) | 2021.06.12 |
| [5분 고등수학] 점과 점사이의 거리 공식 유도 (0) | 2021.06.05 |
| [5분 고등수학] 이차부등식이 항상 성립할 조건 (0) | 2021.05.29 |
| [5분 고등수학] 삼차방정식의 근과 계수의 관계 (0) | 2021.05.23 |




댓글