아르키메데스가 실제 사용한 방법을 이용하여 파이 근사값을 구해봅시다. 먼저 외접 다각형의 둘레길이를 구해보겠습니다. 아르키메데스는 6각형부터 시작했습니다.
1. 외접 6각형
아르키메데스는 원을 하나 그리고, 원의 접선을 긋고 원의 중심에서 접선을 잇는 선분을 그었습니다. 아래와 같습니다.

원의 중심에서 OA와 30도 각도인 선분을 그어 접선과 연결하였습니다. 아르키메데스는 30도라고 하지 않고, 직각의 1/3 이라고 하였습니다.

아르키메데스는 정육각형에서 시작한거 아니냐는 의문이 드는 분들도 있을텐데요. 이 그림이 정육각형을 나타냅니다. AC의 길이는 정육각형의 한 변의 절반을 의미합니다. 위 그림에서 외접 정육각형을 상상해보시면 됩니다. 따라서 AC길이의 12배는 정육각형의 둘레길이입니다. 파이의 범위는 아래와 같이 표현됩니다.
$\frac{12AC}{2OA}>\pi$
AC와 OA의 비율을 구하면 위 부등식을 얻을 수 있는 것입니다.
$OA:AC$ 는 얼마일까요? 우리는 $\sqrt{3}:1$이라는 것을 알고 있지만, 아르키메데스 당시에는 $\sqrt{3}$이 없었습니다. 아르키메데스는 근사값을 구하는 대신 부등식으로 표현하였습니다.
$OA:AC>265:153$
254를 153으로 나누면 1.73202입니다. 루트3의 근사값은 1.73205 입니다. 거의 비슷하죠? 아르키메데스가 이 값을 어떻게 구했는지는 미스테리로 남아있습니다.
여기서 외접하는 정육각형으로 근사시킨 파이값의 범위를 구할 수 있습니다. 위에서 AC는 외접하는 정육각형의 한 변의 길이의 절반입니다. 따라서 AC 길이에 12를 곱하면 외접정육각형 둘레 길이가 됩니다. 이 값을 지름인 2OA 로 나누면 파이의 근사값이 됩니다. 위 부등식에 적용해봅시다.
$\frac{OA}{AC}>\frac{265}{153}$
양변을 뒤집어줍니다. 부등호 방향이 바뀝니다.
$\frac{AC}{OA}<\frac{153}{265}$
분자에 12, 분모에 2를 곱합니다.
$\frac{12AC}{2OA}<\frac{12 \cdot 153}{2 \cdot 265}$
좌변은 파이보다 큰 근사값이므로 아래 부등식이 구해집니다.
$\pi<\frac{12 \cdot 153}{2 \cdot 265}$
계산하면 아래와 같습니다.
$\pi<3.464...$
2. 외접 12각형
이제 정6각형에서, 정12각형으로 증가시켜봅시다. 각도를 15도로 바꾸면 정12각형이 됩니다. 즉 각 COA의 각의 이등분선을 그으면 됩니다.

파이의 범위는 아래와 같이 표현됩니다. 외접 정6각형을 사용했을 때보다 더 좁아진 범위일 겁니다.
$\frac{24AD}{2OA}>\pi$
이제 OA:DA 를 구하면 위 범위를 알 수 있습니다.
OA:DA를 어떻게 구할까요? 아르키메데스는 아래 세가지를 이용하여 OA:DA를 구할 수가 있다는 것을 알았습니다.
OA:CA
OC:AC
유클리드 원론 6권의 3번 성질(각의 이등분선의 성질)
OA:CA는 이미 알고 있습니다. OC:AC부터 구해봅시다.
Step1)
아르키메데스는 OC:AC의 비율을 구했습니다. 2:1이므로 쉽게 구할 수 있습니다.
$OC:CA=306:153$
Step2)
삼각형 COA에 유클리드 원론 6권의 3번성질을 적용합시다. 우리가 중학교 때 배운 성질일 것입니다. 각의 이등분선에 대한 비례식입니다. 아래 등식이 성립합니다.
$OC:OA=CD:DA$
아르키메데스는 위 비례식을 아래 비례식으로 변형했습니다.
$(CO+OA):CA=OA:AD$
변형 과정은 아래와 같습니다. 먼저 비례식을 분수형태로 변형합시다.
$\frac{CO}{OA}=\frac{CD}{DA}$
양변에 1을 더합시다.
$1+\frac{CO}{OA}=1+\frac{CD}{DA}$
통분해줍시다.
$\frac{CO+OA}{OA}=\frac{CD+DA}{DA}$
CD+DA는 CA입니다.
$\frac{CO+OA}{OA}=\frac{CA}{DA}$
양변에 OA를 곱하고, CA로 나눠줍니다.
$\frac{CO+OA}{CA}=\frac{OA}{DA}$
비례식으로 바꾸면 아래와 같습니다.
$(CO+OA):CA=OA:AD$
다시 분수형으로 바꾸고 좌변을 둘로 나눕시다.
$\frac{CO}{CA}+\frac{OA}{CA}=\frac{OA}{DA}$
위에서 언급했듯, 아르키메데스는 부등식 $\frac{OA}{CA}>\frac{265}{153}$ 이 성립한다는 것을 알고 있었습니다. 또한 $\frac{CO}{CA}=\frac{306}{153}$ 입니다. 따라서 아래 부등식이 성립합니다.
$\frac{CO}{CA}+\frac{OA}{CA}=\frac{OA}{DA}>\frac{265}{153}+\frac{306}{153}$
OA:DA로 정리하면 아래와 같습니다.
$OA:DA>571:153$
Step3)
위 부등식을 변형하여 파이 범위를 구해봅시다.
$\frac{24DA}{2OA}<\frac{24 \cdot 153}{2 \cdot 571}$
계산과정은 위와 동일하므로 생략합니다. 결과는 아래와 같습니다.
$\frac{24DA}{2OA}<\frac{24 \cdot 153}{2 \cdot 571}$
계산하면 아래와 같습니다.
$\frac{24DA}{2OA}<3.2154...$
파이값의 범위가 더 좁아졌습니다.
3. 외접 24각형
같은 방법으로 AOD를 수직이등분하는 선을 그어 E를 추가합시다.
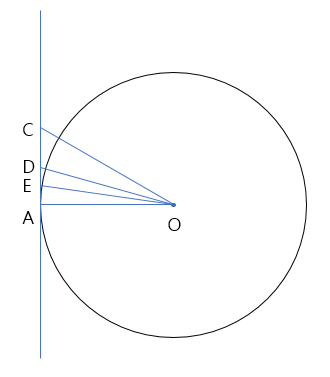
정24각형 파이범위는 아래와 같이 표현됩니다.
$\frac{48AE}{2OA}>\pi$
이제 OA:EA 를 구하면 위 범위를 알 수 있습니다. 아래 세가지를 이용하면 OA:EA를 구할 수가 있습니다.
OA:DA
OD:DA
유클리드 원론 6권의 3번 성질(각의 이등분선의 성질)
OA:DA는 이미 알고 있습니다. OD:DA부터 구해봅시다.
Step1)
피타고라스 정리를 이용하면 아래 등식을 세울 수 있습니다.
$OD^{2}=OA^{2}+AD^{2}$
양변을 $AD^{2}$로 나눠줍니다.
$\frac{OD^{2}}{AD^{2}}=\frac{OA^{2}}{AD^{2}}+1$
$\frac{OA}{DA}>\frac{571}{153}$이므로, 아래 부등식이 성립합니다.
$\frac{OD^{2}}{AD^{2}}= \frac{OA^{2}}{AD^{2}}+1> \left( \frac{571}{153} \right)^{2}+1$
계산하면 아래와 같습니다.
$\frac{OD^{2}}{AD^{2}}=\frac{349450}{23409}$
양변에 루트를 씌워줍니다. 23409는 153을 제곱한 것이므로, 루트를 씌우면 153인데, 349450이 문제입니다. 아르키메데스는 이 값을 $591\frac{1}{8}$ 로 근사시킵니다. 591.125로 근사시킨 것입니다. 실제 루트값을 구해보면 591.1429..이 나옵니다. 따라서 OD와 DA의 비는 아래와 같습니다.
$OD:DA=591\frac{1}{8}:153$
Step2)
삼각형 DOA에 유클리드의 원리에 나오는 각의 이등분선성질을 적용합시다.
$OD:OA=DE:EA$
위 식을 분수형태로 표현하고 양변에 1을 더합시다.
$\frac{OD}{OA}+1=\frac{DE}{EA}+1$
통분해줍시다.
$\frac{OD+OA}{OA}=\frac{DE+EA}{EA}$
DE+EA는 DA이므로 아래와 같이 변형됩니다.
$\frac{OD+OA}{OA}=\frac{DA}{EA}$
양변에 OA를 곱하고,DA로 나눠줍니다.
$\frac{OD+OA}{DA}=\frac{OA}{EA}$
좌변을 둘로 분리합니다.
$\frac{OD}{DA}+\frac{OA}{DA}=\frac{OA}{EA}$
$\frac{OD}{DA}>\frac{591\frac{1}{8}}{153}$ 라는 것은 위에서 구했습니다. $\frac{OA}{DA}=\frac{571}{153}$ 입니다.
따라서 아래 부등식이 성립합니다.
$\frac{OA}{EA}>\frac{1162\frac{1}{8}}{153}$
Step3)
위 부등식을 변형하여 파이 범위를 구해봅시다. 양변의 역수를 취해줍니다.
$\frac{EA}{OA}<\frac{153}{1162\frac{1}{8}}$
아래와 같이 변형합니다.
$\frac{48EA}{2OA}<\frac{48*153}{2*1162\frac{1}{8}}$
계산하면 아래와 같습니다.
$\frac{48EA}{2OA}<3.15972...$
따라서 파이의 범위는 아래와 같습니다.
$\pi<\frac{48EA}{2OA}<3.15972...$
$\pi<3.15972...$
4. 외접 48각형
같은 방법으로 AOE를 수직이등분하는 선을 그어 G를 추가합시다.

정48각형 파이범위는 아래와 같이 표현됩니다.
$\frac{96AF}{2OA}>\pi$
OA:FA 를 구하면 위 범위를 알 수 있습니다. 아래 세가지를 이용하면 OA:FA를 구할 수가 있습니다.
OA:EA
OE:EA
유클리드 원론 6권의 3번 성질(각의 이등분선의 성질)
OA:EA는 이미 알고 있습니다. OE:EA부터 구해봅시다.
Step1)
피타고라스 정리를 이용하면 아래 등식을 세울 수 있습니다.
$OE^{2}=OA^{2}+AE^{2}$
양변을 $AE^{2}$로 나눠줍니다.
$\frac{OE^{2}}{AE^{2}}=\frac{OA^{2}}{AE^{2}}+1$
$\frac{OA}{EA}>\frac{1162\frac{1}{8}}{153}$ 이므로, 아래 부등식이 성립합니다.
$\frac{OE^{2}}{AE^{2}}= \frac{OA^{2}}{AE^{2}}+1> \left( \frac{1162\frac{1}{8}}{153} \right)^{2}+1$
계산하면 아래와 같습니다.
$\frac{OD^{2}}{AD^{2}}=\frac{1373943\frac{33}{64}}{23409}$
양변에 루트를 씌워줍니다. 23409는 153을 제곱한 것이므로, 루트를 씌우면 153인데, $1373943\frac{33}{64}$ 이 문제입니다. 아르키메데스는 이 값을 $1172\frac{1}{8}$ 로 근사시킵니다. 1172.125로 근사시킨 것입니다. 실제 루트값을 구해보면 1172.153..이 나옵니다. 따라서 OE와 EA의 비는 아래와 같습니다.
$OE:EA=1172\frac{1}{8}:153$
Step2)
삼각형 EOA에 유클리드의 원리에 나오는 각의 이등분선성질을 적용합시다.
$OE:OA=EF:FA$
위 식을 분수형태로 표현하고 양변에 1을 더합시다.
$\frac{OE}{OA}+1=\frac{EF}{FA}+1$
통분해줍시다.
$\frac{OE+OA}{OA}=\frac{EF+FA}{FA}$
EF+FA는 EA이므로 아래와 같이 변형됩니다.
$\frac{OE+OA}{OA}=\frac{EA}{FA}$
양변에 OA를 곱하고,EA로 나눠줍니다.
$\frac{OE+OA}{EA}=\frac{OA}{FA}$
좌변을 둘로 분리합니다.
$\frac{OE}{EA}+\frac{OA}{EA}=\frac{OA}{FA}$
$\frac{OE}{EA}>\frac{1162\frac{1}{8}}{153}$ 라는 것은 위에서 구했습니다. $\frac{OA}{EA}=\frac{1162\frac{1}{8}}{153}$ 입니다.
따라서 아래 부등식이 성립합니다.
$\frac{OA}{FA}>\frac{2334\frac{1}{8}}{153}$
Step3)
위 부등식을 변형하여 파이 범위를 구해봅시다. 양변의 역수를 취해줍니다.
$\frac{FA}{OA}<\frac{153}{2334\frac{1}{8}}$
아래와 같이 변형합니다.
$\frac{96FA}{2OA}<\frac{96*153}{2*2334\frac{1}{8}}$
계산하면 아래와 같습니다.
$\frac{96FA}{2OA}<3.15972...$
따라서 파이의 범위는 아래와 같습니다.
$\pi<\frac{96FA}{2OA}<3.14636...$
$\pi<3.14636...$
5. 외접 96각형
같은 방법으로 AOF를 수직이등분하는 선을 그어 G를 추가합시다.

정48각형 파이범위는 아래와 같이 표현됩니다.
$\frac{96AG}{2OA}>\pi$
OA:GA 를 구하면 위 범위를 알 수 있습니다. 아래 세가지를 이용하면 OA:GA를 구할 수가 있습니다.
OA:FA
OF:FA
유클리드 원론 6권의 3번 성질(각의 이등분선의 성질)
OA:FA는 이미 알고 있습니다. OF:FA부터 구해봅시다.
Step1)
피타고라스 정리를 이용하면 아래 등식을 세울 수 있습니다.
$OF^{2}=OA^{2}+AF^{2}$
양변을 $AF^{2}$로 나눠줍니다.
$\frac{OF^{2}}{AF^{2}}=\frac{OA^{2}}{AF^{2}}+1$
$\frac{OA}{FA}>\frac{2334\frac{1}{8}}{153}$ 이므로, 아래 부등식이 성립합니다.
$\frac{OF^{2}}{AF^{2}}= \frac{OA^{2}}{AF^{2}}+1> \left( \frac{2334\frac{1}{8}}{153} \right)^{2}+1$
계산하면 아래와 같습니다.
$\frac{OE^{2}}{AE^{2}}=\frac{5472132\frac{1}{16}}{23409}$
양변에 루트를 씌워줍니다. 23409는 153을 제곱한 것이므로, 루트를 씌우면 153인데, $5472132\frac{1}{16}$ 이 문제입니다. 아르키메데스는 이 값을 $2339\frac{1}{4}$ 로 근사시킵니다. 2339.25로 근사시킨 것입니다. 실제 루트값을 구해보면 2339.2588..이 나옵니다. 따라서 OF와 FA의 비는 아래와 같습니다.
$OF:FA=2339\frac{1}{4}:153$
Step2)
삼각형 FOA에 유클리드의 원리에 나오는 각의 이등분선성질을 적용합시다.
$OF:OA=FG:GA$
위 식을 분수형태로 표현하고 양변에 1을 더합시다.
$\frac{OF}{OA}+1=\frac{FG}{GA}+1$
통분해줍시다.
$\frac{OF+OA}{OA}=\frac{FG+GA}{GA}$
FG+GA는 FA이므로 아래와 같이 변형됩니다.
$\frac{OF+OA}{OA}=\frac{FA}{GA}$
양변에 OA를 곱하고,FA로 나눠줍니다.
$\frac{OF+OA}{FA}=\frac{OA}{GA}$
좌변을 둘로 분리합니다.
$\frac{OF}{FA}+\frac{OA}{FA}=\frac{OA}{GA}$
$\frac{OF}{FA}>\frac{2339\frac{1}{4}}{153}$ 라는 것은 위에서 구했습니다. $\frac{OA}{FA}=\frac{2339\frac{1}{4}}{153}$ 입니다.
따라서 아래 부등식이 성립합니다.
$\frac{OA}{GA}>\frac{4673\frac{1}{2}}{153}$
Step3)
위 부등식을 변형하여 파이 범위를 구해봅시다. 양변의 역수를 취해줍니다.
$\frac{GA}{OA}<\frac{153}{4673\frac{1}{2}}$
아래와 같이 변형합니다.
$\frac{192GA}{2OA}<\frac{192*153}{2*4673\frac{1}{2}}$
2를 약분해줍니다.
$\frac{192GA}{2OA}<\frac{96*153}{4673\frac{1}{2}}$
분자를 계산합니다.
$\frac{192GA}{2OA}<\frac{14688}{4673\frac{1}{2}}$
아르키메데스는 아래와 같이 변형했습니다.
$\frac{192GA}{2OA}<3+\frac{667\frac{1}{2}}{4672\frac{1}{2}}$
우변의 분수항을 약분합시다.
\frac{192GA}{2OA}<3\frac{1}{7}$
따라서 파이의 범위는 아래와 같습니다.
$\pi<\frac{192GA}{2OA}<3\frac{1}{7}$
$\pi<3\frac{1}{7}$
'etc > 쉬운 수학이야기' 카테고리의 다른 글
| 초평면 (Hyperplane) (2) | 2021.03.09 |
|---|---|
| 아르키메데스 방법으로 파이 구하기 (5) 내접 다각형 (0) | 2021.03.08 |
| 왜 원의 넓이를 미분하면 둘레일까? (0) | 2021.03.07 |
| 10일 만에 주식의 신이 되는 방법 (0) | 2021.02.27 |
| 아르키메데스 방법으로 파이 구하기 (3) 자료 출처 (0) | 2021.02.25 |
| 아르키메데스 방법으로 파이 구하기 (2) n각형을 이용한 부등식 세우기 (0) | 2021.02.23 |
| 아르키메데스 방법으로 파이 구하기 (1) 소개 (0) | 2021.02.21 |
| A4 용지의 가로세로 비율의 비밀 (0) | 2021.02.20 |



댓글