지난 글에서 직접 구해본 황금비는 아래와 같습니다.
$\frac{1+\sqrt{5}}{2}:1$
$\frac{1+\sqrt{5}}{2}$는 대략 1.618034 입니다. 따라서 황금비의 근사값은 아래와 같습니다.
1.618:1
가까운 정수비 근사값으로는 8:5, 16:9 가 있습니다.
신용카드 종횡비, 디스플레이 16:9비율, 비너스상 다비드상 비율, 파르테논신전, 앵무조개 등은 황금비의 근사값에 가까운 비율이며 진짜 황금비는 아닙니다.
진짜 황금비 중 하나를 소개합니다. 오각형 별에 들어있는 황금비입니다
정오각형의 꼭지점을 연결하여 만들어지는 별을 펜타그램(pentagram)이라고 합니다.

위 그림에서 a:b, b:c, c:d 는 모두 황금비를 이룹니다.
증명해봅시다. 정오각형의 한 변은 b와 같고, 각도들은 아래와 같습니다.
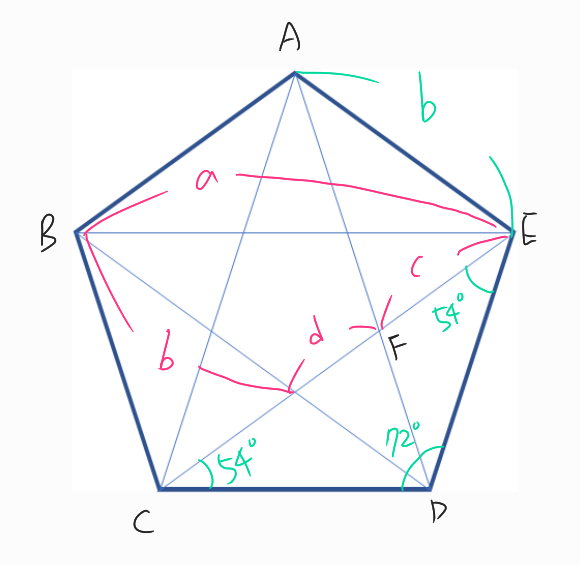
$\bigtriangleup BDE$와 $\bigtriangleup AFE$가 닮음이므로 아래 비례식이 성립합니다.
$a:b=b:c$
외항의 곱은 내항의 곱이므로 아래 등식이 성립합니다.
$b^{2}=ac$
$a=b+c$ 이므로 위 식에 대입하면 아래와 같습니다.
$b^{2}=a(a-b)$
아래와 같이 정리합시다.
$a^{2}-ab-b^{2}=0$
$a$에 대해서 근의공식을 적용하면 아래와 같습니다.
$a=\frac{b\pm \sqrt{b^{2}-4(-b^{2})}}{2}$
아래와 같이 변형합시다.
$a=\frac{b\pm \sqrt{5b^{2}}}{2}$
아래와 같이 변영합시다.
$a=\frac{1\pm \sqrt{5}}{2}b$
$a$는 길이므로 양수입니다.
$a=\frac{1+ \sqrt{5}}{2}b$
따라서 $a:b$는 아래와 같습니다.
$a:b=\frac{1+ \sqrt{5}}{2}b:b$
$a:b=\frac{1+ \sqrt{5}}{2}:1$
나머지 비율인 $b:c$, $c:d$ 도 같은 원리로 구힙니다.
'etc > 쉬운 수학이야기' 카테고리의 다른 글
| 황금비 시리즈 (3) 피보나치수열에 들어있는 황금비 (순한맛) (0) | 2021.05.15 |
|---|---|
| 은행은 복리를 왜 만든걸까? (0) | 2021.05.15 |
| 뉴튼의 일화 (feat. 일론 머스크, 제프 베조스) (0) | 2021.05.15 |
| 평생을 파이(Pi) 구하는데 쓴사람 (0) | 2021.05.14 |
| 황금비 시리즈 (1) 황금비 직접 구해보기 (0) | 2021.04.24 |
| 인간의 심장은 평생 몇번이나 뛸까 (0) | 2021.03.15 |
| 비례식을 이용한 피타고라스정리 증명 (0) | 2021.03.13 |
| 초평면 (Hyperplane) (2) | 2021.03.09 |


댓글