반응형
[모듈식 수학 (상)] 1. 다항식 (14) 조립제법 사용방법
다항식의 나눗셈을 간편하게 할 수는 없을까 라는 의문을 가진 누군가가 더 간편한 방법을 찾아냈습니다. 그 방법이 조립제법입니다. 한가지 예시를 이용하여 조립제법을 사용하는 방법을 설명하겠습니다.
아래 나눗셈을 봅시다.

이 나눗셈을 조립제법을 이용하여 해봅시다. 단계 별로 설명하겠습니다. 일정한 규칙이 반복되는 것이라 금방 익숙해질 것입니다.
먼저 아래와 같이 ㄴ 자 모양을 그려줍니다. 왼쪽에는 나누는 식인 x-2 를 0으로 만드는 값을 적습니다. 오른쪽에는 계수를 적어줍니다.

최고차항의 계수인 2를 아래와 같이 아래쪽으로 내려줍니다.
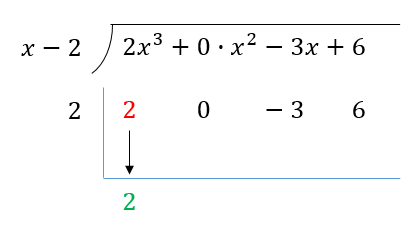
2를 곱하고 0 아래에 써줍니다.
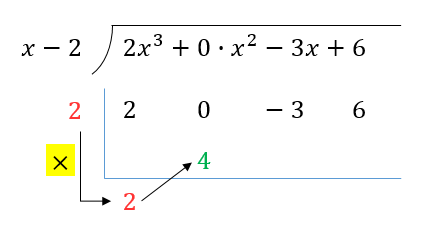
0과 4를 더해줍니다.

2와 4를 곱해서 -3 아래에 써줍니다.

이제 뭘 해야할까요? 이쯤되면 감이 오시나요. -3과 8을 더해서 아래에 써줍니다.

2와 5를 곱해서 6 아래에 써줍니다.

6과 10을 더합니다.
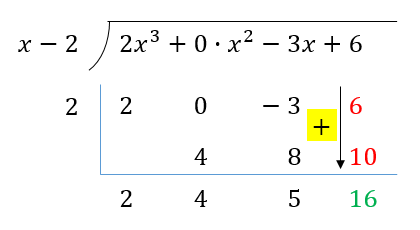
끝입니다. 몫과 나머지는 아래와 같습니다.
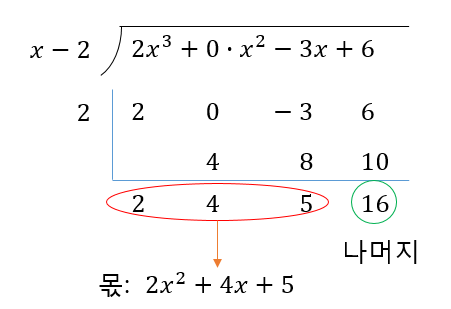
사용해보시면 다항식을 그냥 나눌 때 보다 훨씬 편하다는 것을 알게되실겁니다. 여기서 한가지 의문이 드실텐데요. 조립제법의 원리가 무엇인지 궁금하실겁니다. 다음시간에 알아봅시다.
반응형
'수학(상) > 1. 다항식' 카테고리의 다른 글
| [모듈식 수학 (상)] 1. 다항식 (18) 인수분해 심화유형 (0) | 2018.10.08 |
|---|---|
| [모듈식 수학 (상)] 1. 다항식 (17) 인수분해 기본공식 (0) | 2018.10.08 |
| [모듈식 수학 (상)] 1. 다항식 (16) 다항식의 인수분해란? (0) | 2018.10.08 |
| [모듈식 수학 (상)] 1. 다항식 (15) 조립제법 원리 + 더 편한 방법 소개 (0) | 2018.10.08 |
| [수학 상] (1-13) 나머지정리와 인수정리 (0) | 2018.10.08 |
| [수학 상] (1-12) 다항식의 나눗셈과 항등식 (0) | 2018.10.08 |
| [수학 상] (1-11) 항등식의 정의와 성질 (0) | 2018.10.08 |
| [수학 상] (1-10) 다항식의 나눗셈 (0) | 2018.10.08 |

댓글