원의 접선의 방정식을 구하는 문제 유형에는 세가지가 있습니다.
1) 기울기 m을 알려줄게 접선을 구해보세요
2) 원 위의 한 점을 알려줄게 접선을 구해보세요
3) 원 밖의 한 점을 알려줄게 접선을 구해보세요
두 번째 경우를 구해봅시다. 아래 그림과 같이 중심이 원점이고 반지름이 r인 원 위의 한 점을 알고 있는 상황을 가정합시다. 원 위의 한 점은 $(x_{1},y_{1})$ 입니다.

기울기를 아는 경우에는 접선이 두 개 존재한 반면, 원 위의 한 점을 아는 경우에는 접선이 하나만 존재합니다.

접선의 기울기를 구하기 위해 아래 그림과 같이 원의 중심과 접점을 연결하는 선을 하나 그어봅시다. 이 선은 접선과 수직으로 만납니다.
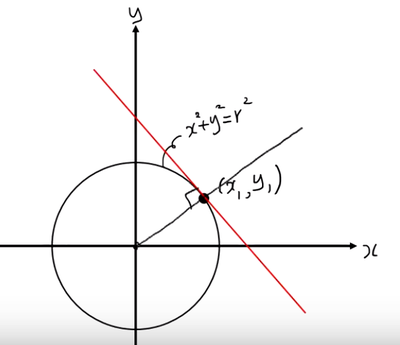
원의 중심과 접점을 연결한 선의 기울기는 아래 그림에서 보이는 것처럼 $\frac{y_{1}}{x_{1}}$ 이라는 것을 쉽게 알 수 있습니다.

원의 중심과 접접을 연결한 직섬은, 접선과 수직 관계이므로 두 기울기를 곱하면 -1이 나옵니다. 이 조건을 이용하면 접선의 기울기는 $-\frac{x_{1}}{y_{1}}$ 라는 것을 알 수 있습니다.
이제 우리는 우리가 구하려는 접선의 기울기와 한 점을 압니다. 따라서 접선의 방정식은 아래와 같습니다.
$y=-\frac{ x_{1} }{ y_{1} }(x-x_{1})+y_{1}$
이번에는 위 접선의 방정식의 모양을 변형해봅시다. 꽤 괜찮은 모양으로 변형할 수 있습니다.
양변에 $y_{1}$을 곱합니다.
$y_{1}y=-x_{1}(x-x_{1})+y_{1}^{2}$
괄호를 풀어줍니다.
$y_{1}y=-x_{1}x+x_{1}^{2}+y_{1}^{2}$
아래와 같이 이항합시다.
$y_{1}y+x_{1}x=x_{1}^{2}+y_{1}^{2}$
$(x_{1},y_{1})$ 은 $x^{2}+y^{2}=r^{2}$ 위의 점이므로 $x_{1}^{2}+y_{1}^{2}=r^{2}$ 이 성립합니다. 따라서 위 식은 아래와 같이 변형할 수 있습니다.
$y_{1}y+x_{1}x=r^{2}$
아래와 같이 자리를 바꿔줍시다.
$x_{1}x+y_{1}y=r^{2}$
정리해 봅시다 원점을 지나고 한점 $(x_{1},y_{1})$ 을 지나는 직선의 방정식은 아래와 같습니다.
$y=-\frac{ x_{1} }{ y_{1} }(x-x_{1})+y_{1}$
또는
$x_{1}x+y_{1}y=r^{2}$
중심이 원점이 아니라 $(a,b)$인 원 위의 한 점 $(x_{1},y_{1})$을 지나는 직선의 방정식은 어떻게 구할까요? 먼저 원의 중심을 원점으로 이동해줍시다. 원 위의 한 점도 함께 이동합니다. 원 위의 한 점은 $(x_{1}-a,y_{1}-b)$ 로 이동됩니다.
이제 중심이 원점인 원 위의 한 점 $(x_{1}-a,y_{1}-b)$ 을 지나는 접선의 방정식을 구해봅시다.
$(x_{1}-a)x+(y_{1}-b)y=r^{2}$
이제 원을 원래 자리로 돌려놓겠습니다. 직선도 함께 이동합니다. x축으로 a만큼, y축으로 b만큼 이동시키면 됩니다.
$(x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}$
'고등수학 5분증명(2009개정) > 수학1' 카테고리의 다른 글
| [5분 고등수학] 원의 접선의 방정식 (3) 원 밖의 한 점을 알 때 (0) | 2021.08.07 |
|---|---|
| [5분 고등수학] 원의 접선의 방정식 (1) 기울기가 m인 경우 (0) | 2021.07.24 |
| [5분 고등수학] 두 원의 공통 내접선의 길이 (0) | 2021.07.17 |
| [5분 고등수학] 두 원의 공통 외접선의 길이 (0) | 2021.07.10 |
| [5분 고등수학] 점과 직선 사이의 거리 (0) | 2021.07.07 |
| [5분 고등수학] 두 직선의 교점을 지나는 직선 (0) | 2021.07.06 |
| [5분 고등수학] 정점을 지나는 직선 (0) | 2021.07.03 |
| [5분 고등수학] 두 직선이 수직일 때의 기울기 (0) | 2021.06.26 |




댓글