반응형
[모듈식 수학 (상)] 1. 다항식 (10) 다항식의 나눗셈
다항식의 나눗셈은 아래와 같이 두가지로 나뉩니다.
- 다항식을 단항식으로 나눔
- 다항식을 다항식으로 나눔
1. 다항식을 단항식을 나눔
A,B,C 를 각각 어떤 단항식이라고 가정합시다. 따라서 A+B 는 다항식이 됩니다. 다항식 A+B 를 단항식 C로 나누는 방법은 아래와 같습니다.
$(A+B)\div C=\frac{A}{C}+\frac{B}{C}$
단항식을 단항식으로 나누면 나머지는 항상 상수입니다.
2. 다항식을 다항식으로 나눔
A,B,C,D 를 각각 어떤 단항식이라고 가정합시다. 따라서 A+B 와 C+D는 다항식입니다. 다항식 A+B를 다항식 C+D로 나누는 방법은 아래와 같습니다.
$(A+B)\div (C+D)=\frac{A+B}{C+D}$
지금부터 배울 3번은 2번의 특수한 경우입니다.
3. 다항식을 다항식으로 나눔 (문자가 한가지인 경우)
문자가 한 가지인 경우는 숫자끼리 나눌 때 처럼 나눗셈을 할 수 있습니다. 1,2번도 불가능한 것은 아닌데 너무 복잡해서 고등학교 범위에서는 다루지 않습니다.
문자가 한가지인 경우에서 다항식을 다항식으로 나누는 예를 한가지 들어보겠습니다.
$(2x^2+3x+1)\div (x+1)$
나눗셈을 하는 방법은 아래 그림과 같습니다. 차수를 '자릿수'라고 생각하고 숫자를 나누듯 나누면 됩니다.
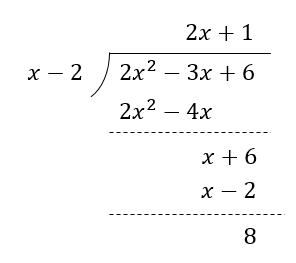
문자가 한가지인 경우에 다항식을 다항식으로 나누면 나머지는 나누는 식(위 경우 $x-2$) 보다 차수가 작습니다. 나머지가 나누는 식과 차수가 같다면 한번 더 나눠줄 수 있고 결국 차수가 나누는 식보다 작아집니다.
반응형
'수학(상) > 1. 다항식' 카테고리의 다른 글
| [수학 상] (1-14) 조립제법 사용방법 (0) | 2018.10.08 |
|---|---|
| [수학 상] (1-13) 나머지정리와 인수정리 (0) | 2018.10.08 |
| [수학 상] (1-12) 다항식의 나눗셈과 항등식 (0) | 2018.10.08 |
| [수학 상] (1-11) 항등식의 정의와 성질 (0) | 2018.10.08 |
| [수학 상] (1-9) 다항식의 곱셈공식 22가지 (0) | 2018.10.08 |
| [수학 상] (1-8) 다항식의 곱셈 (0) | 2018.10.08 |
| [수학 상] (1-7) 다항식의 지수법칙 (0) | 2018.10.08 |
| [수학 상] (1-6) 다항식의 덧셈에 대한 교환법칙과 결합법칙 (0) | 2018.10.08 |

댓글